第五章:PHP编程思想提升篇——递推思想
更新于:2017-04-18 20:23:57
关于递推,从网上找的一段解释:
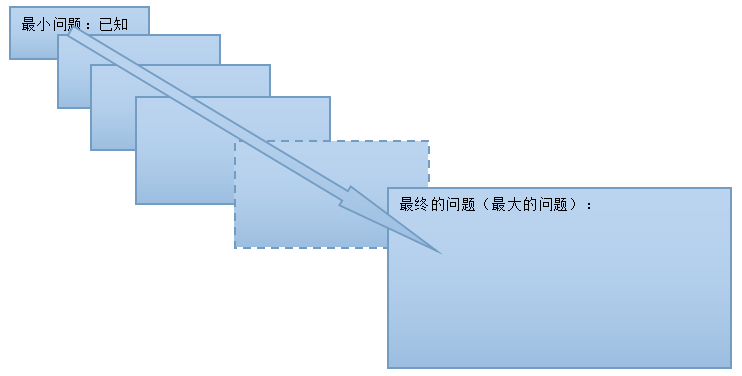
为了解决一个“大”问题,根据现实逻辑,如果能够找到同类问题的一个“最小问题”的答案(通常是已知的),并且根据已知算法,又可以因此得到比最小问题“大一级”问题的答案。 而且,依次类推,又可以得到再大一级问题的答案,最终就可以得到“最大那个问题”(即要解决的问题)的答案。
可见,该思想的过程依赖与2个条件:
1,可知同类最小问题的答案;
2,大一级问题的答案可以通过小一级问题的答案经过简单运算规则而得到。
此思想的解体思路是:从小到大
上面的术语解释理解是不是挺费劲,不管它了,我们直接看示例代码:
求斐波那契数列的第n项的值。
斐波那契数列的规则是:某项的值是其前两项的值的和。
斐波那契数列的前几项为:1,1,2,3,5,8,13,21...(前两项是已知的)
思路:一看这个需求,第一反应先定义一个函数,变量n就是函数的唯一形参。代码里肯定会有for循环,肯定会有两个临时变量。
上代码:
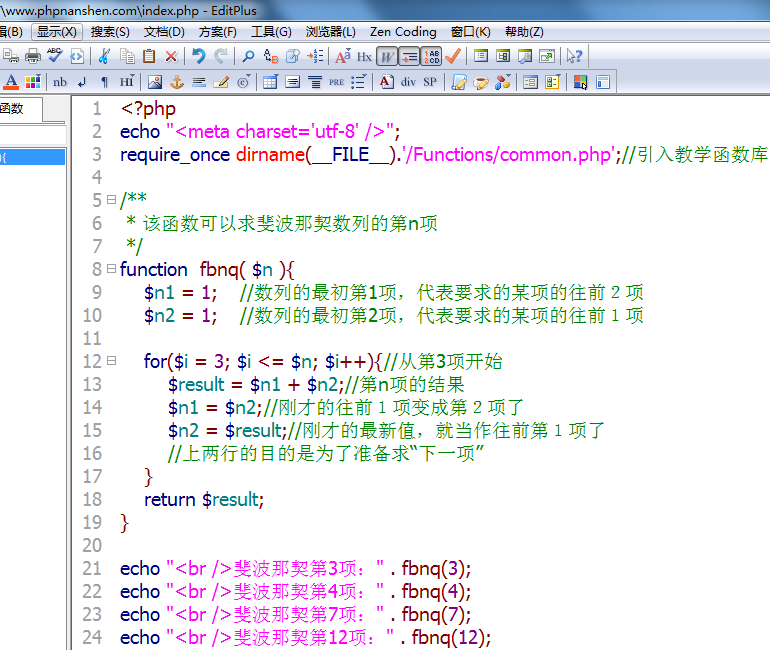
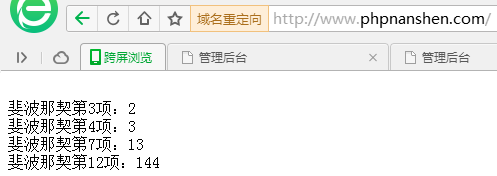
仔细看看代码,应该是非常好理解的。