第五章：PHP编程思想提升篇——选择排序、插入排序

选择排序：

将下列数组进行正序（从小到大）排列出来

$arr = [ 5,  15,  3,  4， 9， 11];

逻辑描述：

第1趟：取得该数组中的最大值及其下标，然后跟该数组的最后一项“交换”（倒数第1项确定）

第2趟：取得该数组中除最后1项中的最大值及其下标，然后跟倒数第2项交换（倒数第2项确定）

第3趟：取得该数组中除最后2项中的最大值及其下标，然后跟倒数第3项交换（倒数第3项确定）

。。。。。。

逻辑描述（假设数组有n项）：

1，要进行n-1趟才可能得出结论

2，每一趟要找的数据的个数都比前一趟少一个，第1趟要找n个

3，每次找出的最大值所在的项，和要与之进行交换的项的位置，依次减1，第一次的位置n-1

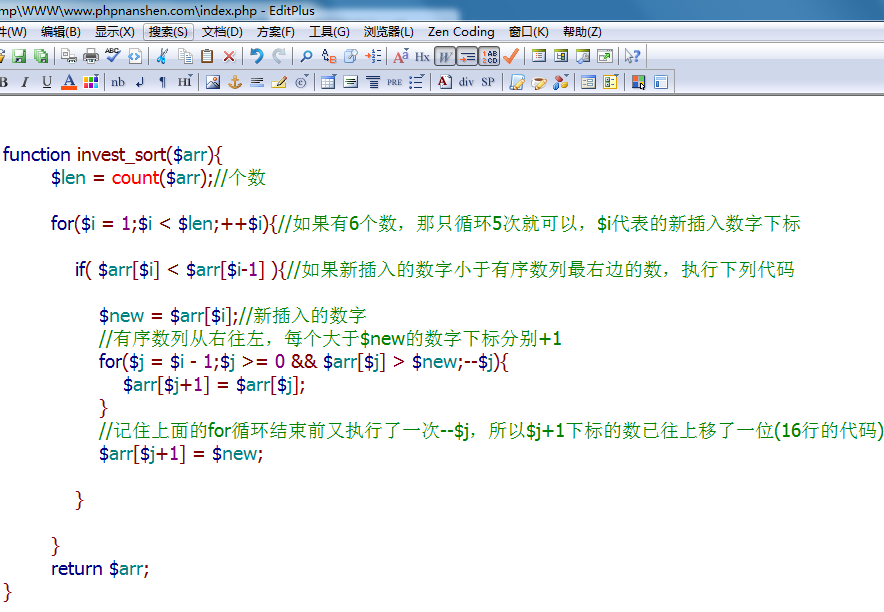
看代码：

选择排序是不稳定的排序方法，大家练的时候可以试着“每一趟先找出最小的，依次放到右边”。

插入排序：

有一个已经有序的数列，要求在这个已经排好的数列中插入一个数，但要求插入后此数列仍然有序，这个时候就要用到一种新的排序方法——插入排序法。

插入排序的基本操作就是将一个数字插入到已经排好序的数列中，从而得到一个新的、个数加一的数列，算法适用于少量数据的排序，是稳定的排序方法。

看这张图：

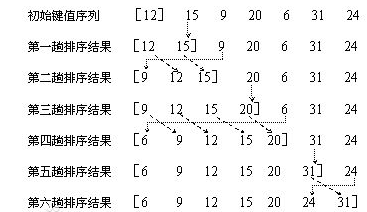
排序前，我们先把第一个数[12]当成一个从小到大的有序数列。

第一趟：把“15”放入有序数列最右边，判断新插入的数字“15”是否小于有序数列最右边的数，不小于那说明“15”是最大，符合有序数列的排序，跳过这一趟。

第二趟：把“9”放入有序数列最右边，判断新插入的数字“9”是否小于有序数列最右边的数，小于那说明“9”不应该放在有序数列最右边，用for循环把“9”放到有序数列合适的位置处。

。。。。。。

看代码:

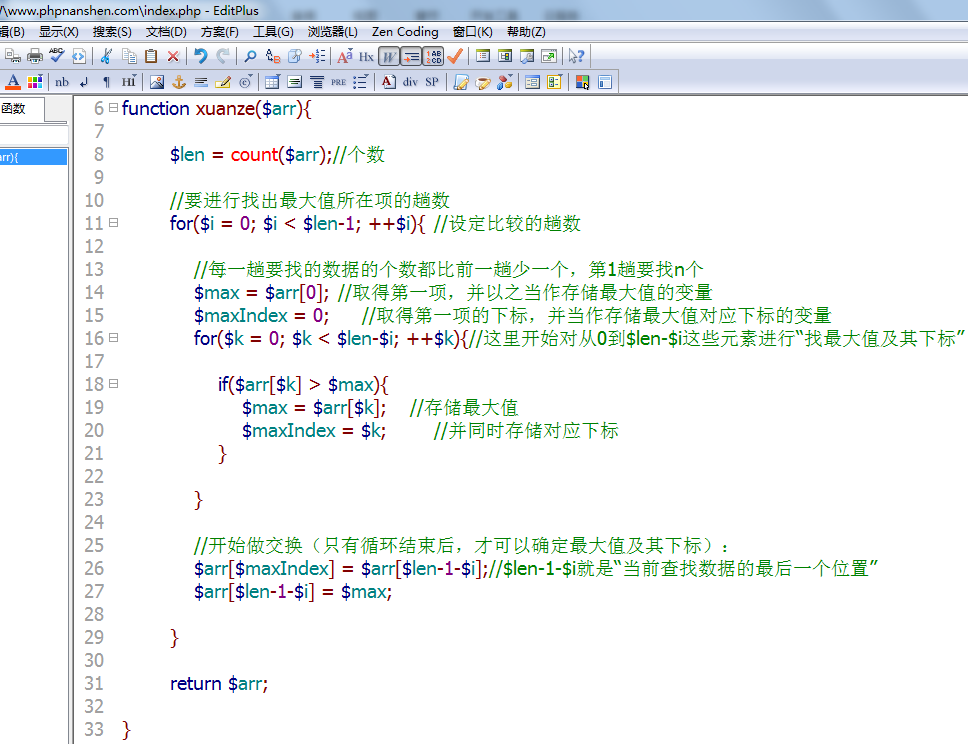
本节学习代码》》》