第三章:二进制、八进制、十六进制与十进制之间的转换
这节课讲解下二进制、八进制、十六进制与十进制之间的转换,你要是不会自己转换的话,其实不影响我们后面的编程。根据楠神的编程经验,基本上用不到我们手工算出来转换的,写的数字全部还是以十进制格式为主,计算机在底层很快能转成二进制。
二进制、八进制、十六进制转换非常简单,如下:
二进制 10010010101 ------》 10 010 010 101 -------》 八进制 2225
说明:10 可以转成 1*2^1 + 0*2^0 = 2
010可以转成 0*2^2 + 1*2^1 + 0*2^0 = 2
010可以转成 0*2^2 + 1*2^1 + 0*2^0 = 2
101可以转成 1*2^2 + 0*2^1 + 1*2^0 = 5
所以10010010101转成八进制是2225
二进制 10010010101 ------》 100 1001 0101 -------》 十六进制 495
说明:100 可以转成 1*2^2 + 0*2^1 + 0*2^0 = 4
1001可以转成 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0 = 9
0101可以转成 0*2^3 +1*2^2 + 0*2^1 + 1*2^0 = 5
所以10010010101转成十六进制是495
记住十六进制的数字包括如下(从0开始):
0 1 2 3 4 5 6 7 8 9 A B C D E F
对应10进制其实是:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
十六进制、八进制转二进制同理,如下:
十六进制 1f34 -------> 1 1111 0011 0100 -----> 二进制 1111100110100
说明:1可以拆分成四位的二进制 0*2^3 +0*2^2 + 0*2^1 + 1*2^0
f可以拆分成四位的二进制 1*2^3 +1*2^2 + 1*2^1 + 1*2^0
3可以拆分成四位的二进制 0*2^3 +0*2^2 + 1*2^1 + 1*2^0
4可以拆分成四位的二进制 0*2^3 +1*2^2 + 0*2^1 + 0*2^0
八进制 2734 -------> 10 111 011 100 -----> 二进制 10111011100
说明:2可以拆分成三位的二进制 0*2^2 + 1*2^1 + 0*2^0
7可以拆分成三位的二进制 1*2^2 + 1*2^1 + 1*2^0
3可以拆分成三位的二进制 0*2^2 + 1*2^1 + 1*2^0
4可以拆分成三位的二进制 1*2^2 + 0*2^1 + 0*2^0
二进制与十进制之间的转换:
二进制转十进制非常简单:
110100 -----》 1*2^5 + 1*2^4 + 0*2^3 + 1*2^2 + 0*2^1 +0*2^1 = 32 + 16 + 4 = 52
十进制转二进制:
基本做法是:将10进制数字除以2,并取得余数,如果除得的商不为0,则继续除以2,并继续去的余数,直到商为0。然后将所有取得的余数,按“倒序写出”,就是对应的2进制数字:
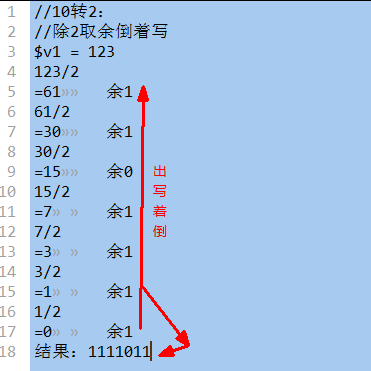
十进制123 -------》 二进制 1111011
学完前面这些,我们完全可以各种进制之间转换了。比如说十进制转十六进制,可以先把十进制转成二进制,再转成十六进制。
直接十进制转十六进制:
基本做法是:将10进制数字除以16,并取得余数,如果除得的商不为0,则继续除以16,并继续去的余数,直到商为0。然后将所有取得的余数,按“倒序写出”,就是对应的16进制数字:

十进制 178 -------》 十六进制 B2
直接十进制转八进制:
基本做法是:将10进制数字除以8,并取得余数,如果除得的商不为0,则继续除以8,并继续去的余数,直到商为0。然后将所有取得的余数,按“倒序写出”,就是对应的8进制数字:

十进制 178 --------》 八进制 262